Tlmivý roztok
| Kyseliny a zásady |
|---|

|
| Acidobázická homeostáza • Acidobázická reakcia • Amfotérna zlúčenina • Autoprotolýza vody • Disociačná konštanta • Extrakcia • Frustrovaný Lewisov pár • Funkcia kyslosti • Hammettova funkcia kyslosti • Chirálna Lewisova kyselina • Katalýza Lewisovou kyselinou • Konjugovaný pár • Kyselina • pH • Protónová afinita • Rovnovážna chémia • Sila kyselín • Titrácia • Tlmivý roztok • Zásada |
| Druhy kyselín |
| Brønsted–Lowry • Lewis • Akceptor • Minerálne • Organické • Oxidy • Silné • Slabé • Superkyseliny • Pevné |
| Druhy zásad |
| Brønsted–Lowry • Lewis • Donor • Organické • Oxidy • Silné • Slabé • Superzásady • Nenukleofilné |
Tlmivý roztok[1] alebo pufer[1] je vodný roztok, ktorý sa skladá zo zmesi slabej kyseliny a jej konjugovanej zásady alebo slabej zásady a jej konjugovanej kyseliny. Ak je k tomuto roztoku pridané malé množstvo silnej kyseliny alebo zásady, pH tohto roztoku sa mení len veľmi málo. Pufre sa používajú ako spôsob udržiavania pH pri takmer konštantných hodnotách v rôznych chemických aplikáciách. V prírode existuje mnoho systémov, ktoré využívajú pufre pre reguláciu pH, napríklad hydrogénuhličitanový tlmivý roztok sa uplatňuje pri regulácii pH v krvi a takisto ako pufer v oceáne.
Fungovanie tlmivých roztokov
[upraviť | upraviť zdroj]
Tlmivé roztoky odolávajú zmenám pH vďaka prítomnosti rovnováhy medzi slabou kyselinou HA a jej konjugovanou zásadou A-:
- HA ⇌ H+ + A-
Keď sa k tejto rovnováhe pridá silná kyselina, pridávajú sa vodíkové katióny (H+), čo posunie chemickú rovnováhu smerom doľava podľa Le Chatelierovho princípu. Kvôli tomu sa koncentrácia vodíkových katiónov zvýši menej, než by sa očakávalo na základe pridaného množstva silnej kyseliny. Podobne, ak sa k roztoku pridá silná zásada, koncentrácia vodíkových katiónov sa zníži menej, než by sa očakávalo podľa pridaného množstva. Na obrázku vpravo je tento efekt ilustrovaný pomocou simulovanej titrácie slabej kyseliny s pKa = 4,7. Relatívna koncentrácia nedisociovanej kyseliny je znázornená modrou farbou a relatívna koncentrácia jej konjugovanej zásady červenou. Zmena pH je relatívne pomalá v tlmenom rozpätí, ktoré je približne pH = pKa ± 1, ktorého stred je pKa = 4,7, kde platí, že [HA] = [A-]. Koncentrácia vodíkových katiónov sa znižuje menej, než by sa očakávalo, pretože väčšina pridaného hydroxidu sa spotrebuje v reakcii
- OH− + HA → H2O + A−
a len malé množstvo sa spotrebuje v neutralizačnej reakcii (teda reakcii, ktorá spôsobí zvýšenie pH)
- OH− + H+ → H2O.
Keď je kyselina deprotonovaná z viac, ako 95 %, pH rastie rýchlo, pretože väčšina pridanej zásady sa využije na neutralizačnú reakciu.
Pufrovacia kapacita
[upraviť | upraviť zdroj]Pufrovacia kapacita je kvantitatívna miera odporu roztoku obsahujúceho pufrovacie činidlo voči zmene pH pri zmene koncentrácie kyseliny alebo zásady. Dá sa vyjadriť nasledovne:[2][3]
kde je nekonečne malé množstvo pridanej zásady, alebo
kde je nekonečne malé množstvo pridanej kyseliny. pH je definované ako −log10[H+] a d(pH) je nekonečne malá zmena pH.
S ktoroukoľvek z týchto definícii sa dá pufrovacia kapacita slabej kyseliny HA s disociačnou konštantou Ka vyjadriť ako[3][4][5]
kde [H+] je koncentrácia vodíkových katiónov a je celková koncentrácia pridanej kyseliny. Kw je rovnovážna konštanta autoprotolýzy vody, ktorá je rovná 1.0×10−14. Pozor na to, že ióny H+ sa v roztoku vyskytujú ako ióny H3O+ (hydrónium) a ďalšia solvatácia hydrónia má zanedbateľný efekt na rovnováhu disociácie, okrem prípadov s veľmi vysokou koncentráciou kyseliny.

Táto rovnica ukazuje tri oblasti zvýšenej pufrovacej kapacity (obrázok vpravo):
- V strednej oblasti krivky (znázornená zelenou farbou) je dominantný druhý člen, . Pufrovacia kapacita sa zvyšuje po lokálne maximum pri pH = pKa. Výška tohto píku je závislá na hodnote pKa. Pufrovacia kapacita je zanedbateľná, keď je koncentrácia [HA] tlmiaceho činidla veľmi malá, a zvyšuje sa so zvyšujúcou koncentráciou tlmiaceho činidla.[3] Niektorí autori ukazujú len túto časť grafu pri popise pufrovacej kapacity.[2] Pufrovacia kapacita sa znižuje na 33 % maximálnej hodnoty pri pH = pKa ± 1, na 10 % pri pH = pKa ± 1.5 a na 1 % pri pH = pKa ± 2. Kvôli tomu je najpoužiteľnejšie rozpätie približne pH = pKa ± 1. Pri vyberaní pufru na použitie pri konkrétnom pH by sa teda mal zvoliť pufer s hodnotou pKa čo najbližšie k zvolenému pH. [2]
- Pri veľmi kyslých roztokoch s pH menej než ~2 (znázornené červenou farbou na obrázku) je dominantný prvý člen, takže sa kapacita exponenciálne zvyšuje so znižujúcim sa pH: . To vyplýva z toho, že druhý a tretí člen sú zanedbateľné pri veľmi nízkom pH. Tento člen je nezávislý na (ne)prítomnosti tlmivého činidla.
- Pri veľmi zásaditých roztokoch s pH viac než ~12 (znázornené modrou farbou na obrázku) je dominantný tretí člen, takže sa kapacita exponenciálne zvyšuje so zvyšujúcim sa pH: . To vyplýva z toho, že prvý a druhý člen sú zanedbateľné pri veľmi vysokom pH. Tento člen je takisto nezávislý na (ne)prítomnosti tlmivého činidla.
Použitie tlmivých roztokov
[upraviť | upraviť zdroj]pH roztokov, ktoré obsahujú tlmivé činidlo, sa môže meniť len v úzkom rozsahu pH, bez ohľadu na to, čo je prítomné v roztoku. V biologických systémoch je toto nutnou podmienkou pre správne fungovanie enzýmov. V ľudskej krvi je napríklad prítomná zmes kyseliny uhličitej (H2CO3) a hydrogénuhličitanu (HCO3-) v plazme. To je hlavný spôsob, ktorým sa udržiava pH krvi medzi 7,35 a 7,45. Mimo tohto úzkeho rozpätia (7,40 ± 0,05) sa rýchlo dostavujú metabolické príznaky acidózy alebo alkalózy, ktoré vedú k smrti, ak sa dostatočne rýchlo neobnoví pufrovacia kapacita krvi.
Ak sa hodnota pH roztoku zmení príliš rýchlo, účinnosť enzýmov sa v procese zníži, čo sa označuje ako denaturácia (strata pôvodnej štruktúry), ktorá je zvyčajne nevratná.[6] Väčšina biologických vzoriek používaných vo výskume sa udržiava v tlmivov roztoku, bežne vo fosfátovom pufri (PBS) pri pH 7,4.
V priemysle sa používajú tlmivé roztoky počas fermentačných procesoch a pri nastavovaní správnych podmienok pre použitie farbív vo farbení látok. Takisto sa používajú pri chemickej analýze[5] a kalibrácii pH metrov.
Jednoduché tlmivé roztoky
[upraviť | upraviť zdroj]Tlmivý roztok pKa Použiteľné rozpätie pH Kyselina citrónová 3,13, 4,76, 6,40 2,1–7,4 Kyselina octová 4,8 3,8–5,8 KH2PO4 7,2 6,2–8,2 CHES 9,3 8,3–10,3 Borát 9,24 8,25–10,25
Pre úpravu pH tlmivých roztokov v kyslej oblasti je možné použiť prídavok silnej kyseliny, napríklad kyseliny chlorovodíkovej, k zvolenému tlmivému roztoku. U zásaditých tlmivých roztokov je možné pridať silnú zásadu, napríklad hydroxid sodný. Okrem toho je možné pripraviť tlmivý roztok z kyseliny a jej konjugovanej zásady. Napríklad acetátový pufer je možné pripraviť ako roztok kyseliny octovej a octanu sodného. Podobným spôsobom je možné pripraviť zásaditý pufer zo zásady a jej konjugovanej kyseliny.
„Univerzálne“ tlmivé roztoky
[upraviť | upraviť zdroj]Zmiešaním zlúčenín, ktorých pKa hodnoty sa líšia o dve alebo menej jednotiek, a úpravou pH je možné získať tlmivé roztoky so širokými rozpätiami. Kyselina citrónová je užitočnou súčasťou tlmivých roztokov, pretože má tri hodnoty pKa, ktoré sa od seba líšia o menej než dve jednotky. Pufrovacie rozpätie sa dá rozšíriť pridaním ďalších tlmivých činidiel. Nasledujúce roztoky (McIlvainov pufer) má pufrovacie rozmedzie od 3 do 8.[7]
0,2 M Na2HPO4 (ml) 0,1 M kyselina citrónová (ml) pH 20,55 79,45 3,0 38,55 61,45 4,0 51,50 48,50 5,0 63,15 36,85 6,0 82,35 17,65 7,0 97,25 2,75 8,0
Roztok obsahujúci kyselinu citrónovú, dihydrogénfosforečnan draselný, kyselinu boritú a kyselinu dietylbarbiturovú môže pokryť pH rozpätie od 2,6 až po 12.[8] Medzi ďalšie univerzálne tlmivé roztoky patria Carmodyho pufer[9] a Britton-Robinsonov pufer, vyvinutý v roku 1931.
Tlmivé roztoky bežne používané v biológii
[upraviť | upraviť zdroj]Pre efektívne rozpätie, pozri pufrovaciu kapacitu vyššie.
| Bežný názov
(chemický názov) |
Štruktúra | pKa, 25 °C |
Teplotný efekt, dpH/dT (K−1)[10] |
Molekulárna
hmotnosť |
|---|---|---|---|---|
| TAPS (kyselina [tris(hydroxymetyl)metylamino]propánsulfónová) |
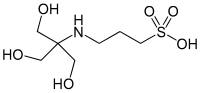
|
8,43 | −0,018 | 243,3 |
| Bicín (kyselina 2-(bis(2-hydroxyetyl)amino)octová) |

|
8,35 | −0,018 | 163,2 |
| Tris (tris(hydroxymetyl)aminometán alebo 2-amino-2-(hydroxymetyl)propán-1,3-diol) |

|
8,07[Pozn. 1] | −0,028 | 121,14 |
| Tricín (N-[tris(hydroxymetyl)metyl]glycín) |
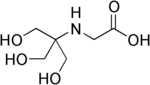
|
8,05 | −0,021 | 179,2 |
| TAPSO (kyselina 3-[N-tris(hydroxymetyl)metylamino]-2-hydroxypropánsulfónová) |

|
7,635 | 259,3 | |
| HEPES (kyselina 4-(2-hydroxyetyl)-1-piperazínetánsulfónová) |

|
7,48 | −0,014 | 238,3 |
| TES, (kyselina 2-[[1,3-dihydroxy-2-(hydroxymetyl)propán-2-yl]amino]etánsulfónová) |
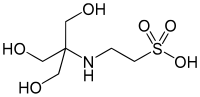
|
7,40 | −0,020 | 229,20 |
| MOPS (kyselina 3-(N-morfolíno)propánsulfónová) |

|
7,20 | −0,015 | 209,3 |
| PIPES (piperazín-N,N′-bis(2-etánsulfónová kyselina)) |
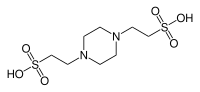
|
6,76 | −0,008 | 302,4 |
| Kakodylát (kyselina dimetylarzeničná) |
|
6,27 | 138,0 | |
| MES (kyselina 2-(N-morfolíno)etánsulfónová) |
|
6,15 | −0,011 | 195,2 |
- ↑ Tris je zásada, toto pKa odpovedá jej konjugovanej kyseline.
Výpočet pufrovacieho pH
[upraviť | upraviť zdroj]Monoprotické kyseliny
[upraviť | upraviť zdroj]Pre monoprotické kyseliny (kyseliny, ktoré odštepujú len jeden katión vodíka) je nutné si najprv napísať rovnovážnu reakciu:
- HA ⇌ A− + H+
Tá ukazuje, že keď sa kyselina štiepi, vzniká rovnaké množstvo aniónov a vodíkových katiónov. Rovnovážne koncentrácie týchto troch zložiek je možné spočítať pomocou nasledujúcej tabuľky:
[HA] [A−] [H+] Počiatočná konc. C0 0 y Zmena konc. −x x x Koncová konc. C0 − x x x + y
Prvý riadok ukazuje podmienky na začiatku procesu: koncentrácia kyseliny je C0, na začiatku nedisociovaná, takže koncentrácia A- a H+ by bola nulová. y je počiatočná koncentrácia pridanej silnej kyseliny, napríklad kyseliny chlorovodíkovej. Ak sa pridáva silná zásada, napríklad hydroxid sodný, tak y bude mať zápornú hodnotu, pretože zásada odstraňuje vodíkové katióny z roztoku.
Druhý riadok ukazuje, ako sa mení hodnota jednotlivých zložiek počas disociácie kyseliny. Koncentrácia kyseliny sa zníži o x, teda sa zmení o -x, a koncentrácie A- i H+ sa zvýšia o +x. Tieto zmeny vychádzajú z rovnovážnej rovnice.
Tretí riadok ukazuje stav v rovnováhe a je súčtom prvých dvoch riadkov.
Aby bolo možné zistiť x, je nutné použiť rovnicu pre rovnovážnu konštantu vyjadrenú pomocou koncentrácií:
Do tejto rovnice sa dosadia hodnoty z posledného riadku tabuľky:
Čo je možné zapísať ako
Pre známe hodnoty C0, Ka a y je možné túto rovnicu spočítať a zistiť x. Keďže platí pH = −log10[H+], je možné pH zistiť ako pH = −log10(x + y).
Polyprotické kyseliny
[upraviť | upraviť zdroj]
Polyprotické kyseliny sú schopné odštiepiť viac než jeden vodíkový katión. Disociačná konštanta pre prvý vodíkový katión sa označuje ako Ka1, disociačná konštanta pre druhý vodíkový katión sa označuje ako Ka2 a tak ďalej. Príkladom polyprotickej kyseliny je kyselina citrónová, ktorá je schopná odštiepiť až tri vodíkové katióny a je teda možné ju zaznačiť ako H3A.
Rovnovážna reakcia Hodnota pKa pre kyselinu citrónovú H3A ⇌ H2A− + H+ pKa1 = 3,13 H2A− ⇌ HA2− + H+ pKa2 = 4,76 HA2− ⇌ A3− + H+ pKa3 = 6,40
Keď je rozdiel medzi po sebe idúcimi hodnotami pKa menší než 3, tak sa prekrývajú rozpätia pH, v ktorých sú prítomné jednotlivé zlúčeniny počas rovnováhy. Čím menší je tento rozdiel, tým výraznejší je prekryv. V prípade kyseliny citrónovej je tento prekryv výrazný a roztoky kyseliny citrónovej majú tlmivé schopnosti v rozmedzí pH 2,5 až 7,5.
Výpočet pH polyprotických kyselín vyžaduje výpočet koncentrácií všetkých prítomných zlúčenín. Pre prípad kyseliny citrónovej to znamená riešenie dvoch rovníc zachovania hmotnosti:
CA je analytický koncentrácia kyseliny, CH je potom analytická koncentrácia pridaných vodíkových katiónov, βq sú kumulatívne asociačné konštanty, Kw je konštanta autoprotolýzy vody. Tým vzniká sústava dvoch nelineárnych rovníc s neznámymi [A3−] a [H+]. Sú dostupné mnohé počítačové programy, ktoré tieto rovnice spočítajú. Diagram pre kyselinu citrónovú na obrázku vyššie bol vytvorený v programe HySS.[11] Kumulatívne asociačné konštanty sú číslované v opačnom poradí, ako jednotlivé disociačné konštanty. Vzťah medzi kumulatívnymi asociačnými konštantami (β) a postupnými disociačnými konštantami (K) v prípade triprotickej kyseliny je uvedený v nasledujúcej tabuľke:
Rovnováha Vzťah A3− + H+ ⇌ AH2+ log β1= pka3 A3− + 2H+ ⇌ AH2+ log β2 =pka2 + pka3 A3− + 3H+ ⇌ AH3 log β3 = pka1 + pka2 + pka3
Kumulatívne asociačné konštanty sa používajú vo všeobecných počítačových programov, ako napríklad v programe použitom na získanie diagramu vyššie.
Referencie
[upraviť | upraviť zdroj]- ↑ a b Môžem používať v odbornej terminológii (... | Jazyková poradňa | SME.sk [online]. jazykovaporadna.sme.sk, [cit. 2022-05-01]. Dostupné online.
- ↑ a b c SKOOG, Douglas A.; WEST, Donald M.; HOLLER, F. James. Fundamentals of Analytical Chemistry. 9th. vyd. [s.l.] : Brooks/Cole, 2014. ISBN 978-0-495-55828-6. S. 226.
- ↑ a b c Understanding, Deriving and Computing Buffer Capacity. Journal of Chemical Education, 2000, s. 1640–1644. DOI: 10.1021/ed077p1640.
- ↑ BUTLER, J. N.. Ionic Equilibrium: Solubility and pH calculations. [s.l.] : Wiley, 1998. ISBN 978-0-471-58526-8. S. 133–136.
- ↑ a b HULANICKI, A.. Reactions of acids and bases in analytical chemistry. [s.l.] : Horwood, 1987. ISBN 978-0-85312-330-9.
- ↑ SCORPIO, R.. Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems. [s.l.] : [s.n.], 2000. ISBN 978-0-7872-7374-3.
- ↑ MCILVAINE, T. C.. A buffer solution for colorimetric comparaison. J. Biol. Chem., 1921, s. 183–186. Dostupné online. DOI: 10.1016/S0021-9258(18)86000-8.
- ↑ MENDHAM, J.; DENNY, R. C.; BARNES, J. D.. Vogel's textbook of quantitative chemical analysis. 5th. vyd. Harlow : Pearson Education, 2000. ISBN 978-0-582-22628-9. Appendix 5.
- ↑ CARMODY, Walter R.. Easily prepared wide range buffer series. J. Chem. Educ., 1961, s. 559–560. DOI: 10.1021/ed038p559.
- ↑ Buffer Reference Center [online]. Sigma-Aldrich. Dostupné online. Archivované 2009-04-17 z originálu.
- ↑ Hyperquad simulation and speciation (HySS): a utility program for the investigation of equilibria involving soluble and partially soluble species. Coordination Chemistry Reviews, 1999, s. 311–318. Dostupné online. DOI: 10.1016/S0010-8545(98)00260-4.
Pozri aj
[upraviť | upraviť zdroj]Zdroj
[upraviť | upraviť zdroj]Tento článok je čiastočný alebo úplný preklad článku Buffer solution na anglickej Wikipédii.





![{\displaystyle \beta =2.303\left([{\ce {H+}}]+{\frac {T_{{\ce {HA}}}K_{a}[{\ce {H+}}]}{(K_{a}+[{\ce {H+}}])^{2}}}+{\frac {K_{\text{w}}}{[{\ce {H+}}]}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf8b7c2c34d12f8145df3299a061593aaa76643a)

![{\displaystyle \beta \approx 2.303{\frac {T_{{\ce {HA}}}K_{a}[{\ce {H+}}]}{(K_{a}+[{\ce {H+}}])^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52375261c647c1e7460c352b12001fd1a21a146b)


![{\displaystyle K_{\text{a}}={\frac {[{\ce {H+}}][{\ce {A-}}]}{[{\ce {HA}}]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89cb17f8ab679cc14a5d23888ed230c1a71b7384)


![{\displaystyle {\begin{aligned}C_{{\ce {A}}}&=[{\ce {A^3-}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3},\\C_{{\ce {H}}}&=[{\ce {H+}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+2\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+3\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3}-K_{\text{w}}[{\ce {H+}}]^{-1}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/611bf20542dfc1dbd8256ee6465883f1534f527a)