Obelisk (geometria)
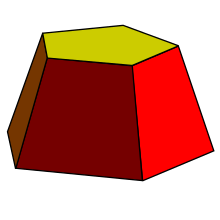
Obelisk je mnohosten,[1] vykonštruovaný dvoma paralelnými mnohouholníkmi, ktorých bočné steny sú lichobežníky.[1] Jedná sa o zrezaný ihlan s mnohouholníkovou podstavou.
Ide o 3-rozmerný priestorový útvar v euklidovskej geometrii. Najbežnejšie sú obelisky s podstavou štvorca, obdĺžnika, trojuholníka, päťuholníka či šesťuholníka, no známe sú aj obelisky s podstavou osemuholníka či desaťuholníka. Takmer všetky obelisky sú mnohosteny, s výnimkou tzv. zrezaného kužeľa,[2] ktorého podstava je kruh,[2] no možná je aj podstava elipsy[3] podobne ako u eliptického valca.[4] Žiaden obelisk s mnohouholníkovou podstavou nemožno vytvoriť rotáciou. Naopak, obelisk s kruhovou podstavou je možné vytvoriť okrem zrezania čiapky kužeľa, aj rotáciou pravouhlého lichobežníka.
Vlastnosti
[upraviť | upraviť zdroj]Každý obelisk s podstavou mnohouholníka sa radí medzi prismatoidy. Vďaka tomu, že jeho plášť tvoria lichobežníky, spadá daný prismatoid pod skupinu obeliskov. Všeobecne platí, že mnohouholník či kruh hornej podstavy musí byť -krát menší, než mnohouholník či kruh dolnej podstavy. V prípade, že sú obe podstavy rovnako veľké, ich plášť nemôže byť tvorený lichobežníkmi, ale obdĺžnikmi čo stvorcami, čo je hranol, nie obelisk. To isté platí aj v prípade kruhovej podstavy. Ak sú kruhy oboch podstáv rovnako veľké, jedná sa o valec, nie obelisk (v tomto prípade zrezaný kužeľ). Aj v prípade že dve eliptické podstavy sú rovnako veľké, vzniká eliptický valec. Obelisky sú útvary konvexné. Ďalej existujú nepravidelné obelisky, ktoré majú za podstavy nepravidelné mnohouholníky a majú teda neurčité tvary plášťa.
Druhy pravidelných obeliskov
[upraviť | upraviť zdroj]Základný (štvorcový) obelisk
[upraviť | upraviť zdroj]Je tvorený dvoma paralelnými štvorcami tvoriacich dolnú a hornú podstavu. Plášť tohto obelisku tvoria 4 rovnoramenné lichobežníky, ktorých dĺžka strany (dolná, najdlhšia strana) je zhodná s dĺžkou strany v dolnej podstave štvorca.[5] Toto isté tvrdenie platí aj na hornú stranu lichobežníka ktorá je zhodná s dĺžkou strany v hornej podstave štvorca. Preto:
- a
Obvod dolnej podstavy vypočítame ako:
Obvod hornej podstavy vypočítame ako:
Objem vypočítame ako:[5]
Obsah plášťa vypočítame ako:
Pretože obsah lichobežníka vypočítame ako , a plášť základného obelisku tvoria 4 rovnaké rovnoramenné lichobežníky, stačí iba obsah lichobežníka vynásobiť štyrmi. Povrch vypočítame ako:
kde:
- je strana hornej štvorcovej podstavy
- je dolná, najdlhšia strana rovnoramenného lichobežníka
- je horná, najkratšia strana rovnoramenného lichobežníka
- je strana dolnej štvorcovej podstavy
- je výška
- je obsah lichobežníka
- je obsah dolnej podstavy
- je obsah hornej podstavy
Obdlžníkový obelisk
[upraviť | upraviť zdroj]Je tvorený dvoma paralelnými obdlžníkmi tvoriacich dolnú a hornú podstavu. Plášť tohto obelisku tvoria 4 rovnoramenné lichobežníky, niesu však všetky rovnaké. Sú to 2 paralelné predné lichobežníky ktorých horná, najkratšia strana je rovnako dlhá ako najdlhšia strana hornej podstavy .[1] Ďalej sú tu 2 bočné lichobežníky ktorých horná, najkratšia strana je rovnako dlhá ako bočná, najkratšia strana hornej obdlžníkovej podstavy, . Ďalej najdlhšia, dolná strana predných lichobežníkov je rovnako dlhá ako najdlhšia strana dolnej podstavy . To isté platí aj pre bočné lichobežníky, ktorých najdlhšie, dolné strany sú rovnako dlhé ako bočné strany dolnej podstavy, . Preto:
- , , a
Obvod dolnej podstavy vypočítame ako:
Obvod hornej podstavy vypočítame ako:
Objem vypočítame ako:[1]
Alebo ako:
Obsah plášťa vypočítame ako:
Povrch vypočítame ako:
kde:
- je najdhlšia strana hornej podstavy (predná strana)
- je najkratšia strana hornej podstavy (bočná strana)
- je najdhlšia strana dolnej podstavy (predná strana)
- je najkratšia strana dolnej podstavy (bočná strana)
- je horná, najkratšia strana predných lichobežníkov
- je horná, najkratšia strana bočných lichobežníkov
- je dolná, najdlhšia strana predných lichobežníkov
- je dolná, najdhlšia strana bočných lichobežníkov
- je výška
Rovnostranný trojuholníkový obelisk
[upraviť | upraviť zdroj]Je tvorený dvoma paralelnými rovnostrannými trojuholníkmi tvoriacich dolnú a hornú podstavu. Plášť tohto obelisku tvoria 3 rovnoramenné lichobežníky. Každá stena je priamo prepojená s ďalšími dvomi, vďaka vlastnosti trojuholníku. Z geometrického hľadiska, ide o zrezaný pravidelný štvorsten. Vďaka tomu že podstava je rovnostranný trojuholník, existuje len strana hornej podstavy a dolnej podstavy . Horná, najkratšia strana lichobežníka je rovnako dlhá ako strana . Dolná, najdlhšia strana lichobežníka je rovnako dlhá ako strana dolnej podstavy . Preto:
- a
Obvod dolnej podstavy vypočítame ako:
Obvod hornej podstavy vypočítame ako:
Objem vypočítame ako:
Obsah plášťa vypočítame ako:
Povrch vypočítame ako:
kde:
- je strana hornej podstavy
- je strana dolnej podstavy
- je horná, najkratšia strana lichobežníka
- je dolná, najdlhšia strana lichobežníka
- je obsah hornej podstavy
- je obsah dolnej podstavy
- je výška
Pentagonálny obelisk
[upraviť | upraviť zdroj]Je tvorený dvoma paralelnými pravidelnými konvexnými päťuholníkmi tvoriacich dolnú a hornú podstavu. Plášť tohto obelisku tvorí 5 rovnoramenných lichobežníkov. Vďaka tomu že ide o pravidelný konvexný polygón s rovnakými dĺžkami strán, existujú len strana hornej podstavy a strana dolnej podstavy .[6] Najkratšia, horná strana lichobežníka má takú istú dĺžku ako strana hornej podstavy . Najdlhšia, dolná strana lichobežníka má takú istú dĺžku ako strana dolnej podstavy . Preto:
- a
Obvod dolnej podstavy vypočítame ako:
Obvod hornej podstavy vypočítame ako:
Objem vypočítame ako:[6]
Obsah plášťa vypočítame ako:
Povrch vypočítame ako:
kde:
- je strana hornej podstavy
- je strana dolnej podstavy
- je horná, najkratšia strana lichobežníka
- je dolná, najdlhšia strana lichobežníka
- je obsah hornej podstavy
- je obsah dolnej podstavy
- je výška
Hexagonálny obelisk
[upraviť | upraviť zdroj]Je tvorený dvoma paralelnými pravidelnými konvexnými hexagónmi (šesťuholníkmi) tvoriacich dolnú a hornú podstavu. Plášť tohto obelisku tvorí 6 rovnoramenných lichobežníkov. Vďaka vyššie uvedenej vlastnosti pravidelných konvexných polygónov s rovnakými dĺžkami strán, existujú len strana hornej podstavy a strana dolnej podstavy . Najkratšia, horná strana lichobežníka má takú istú dĺžku ako strana hornej podstavy . Najdlhšia, dolná strana lichobežníka má takú istú dĺžku ako strana dolnej podstavy . Preto:
- a
Obvod dolnej podstavy vypočítame ako:
Obvod hornej podstavy vypočítame ako:
Na výpočet objemu znova použijeme vzorec na výpočet objemu obeliskov s podstavou pravidelného konvexného polygónu a pod.:
Obsah plášťa vypočítame ako:
Povrch vypočítame ako:
kde:
- je strana hornej podstavy
- je strana dolnej podstavy
- je horná, najkratšia strana lichobežníka
- je dolná, najdlhšia strana lichobežníka
- je obsah hornej podstavy
- je obsah dolnej podstavy
- je výška
Zrezaný kužeľ
[upraviť | upraviť zdroj]Je objekt zkonštruovaný rotáciou pravouhlého lichobežníka o 360°.[2] Jedná sa o špeciálny typ obelisku, kedže sa nezakladá na polygonálnej (mnohouholníkovej) podstave.
Je tvorený dvoma paralelnými kruhmi. Jeho plášť je výsledkom zrezania kužeľa.[2] Obvod dolnej podstavy vypočítame ako:
Obvod hornej podstavy vypočítame ako:
Objem vypočítame ako:[2]
Bočnú stranu kužeľa vypočítame ako:
Obsah plášťa vypočítame ako:
Alebo ako:[2]
Povrch vypočítame ako:
Alebo ako:[2]
kde:
- je polomer dolnej podstavy
- je polomer hornej podstavy
- je výška
Referencie
[upraviť | upraviť zdroj]- ↑ a b c d Volume of a obelisk Calculator [online]. High accuracy calculation for life or science., [cit. 2021-12-07]. Dostupné online. Archivované 2021-12-07 z originálu. (po anglicky)
- ↑ a b c d e f g Volume of a circular truncated cone Calculator [online]. High accuracy calculation for life or science., [cit. 2021-12-21]. Dostupné online. Archivované 2021-12-21 z originálu. (po anglicky)
- ↑ High accuracy calculation for life or science. [online]. keisan.casio.com, [cit. 2021-12-21]. Dostupné online. Archivované 2021-12-21 z originálu.
- ↑ Volume of an elliptic truncated cone Calculator [online]. High accuracy calculation for life or science., [cit. 2021-12-21]. Dostupné online. Archivované 2021-12-21 z originálu. (po anglicky)
- ↑ a b Volume of a truncated square pyramid Calculator [online]. High accuracy calculation for life or science., [cit. 2021-12-21]. Dostupné online. Archivované 2021-12-21 z originálu. (po anglicky)
- ↑ a b Volume of a frustum Calculator [online]. High accuracy calculation for life or science., [cit. 2021-12-21]. Dostupné online. Archivované 2021-12-21 z originálu. (po anglicky)



























![{\displaystyle V_{2}={\frac {1}{6}}h[AB+ab+(A+a)(B+b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a967f943e1abf69fd4eb9f9d417be9bba4381ff)






















