Pascalov trojuholník

Pascalov trojuholník je geometrické usporiadanie kombinačných čísel do tvaru trojuholníka.

História Pascalovho trojuholníka

Pascalov trojuholník sa v matematike preslávil vďaka svojej symetrii a rôznym skrytým vzťahom. Blaise Pascal si v roku 1653 myslel to isté a poznamenal, že by ich pravdepodobne nevedel opísať v jednej práci. Množstvo prepojení Pascalovho trojuholníka s inými vetvami matematiky urobilo z neho posvätný matematický objekt. Jeho korene však siahajú do dávnejšej histórie. V skutočnosti ho neobjavil Pascal, hoci sa po ňom volá. Bol známy už čínskym učencom z 13. storočia.

Schéma

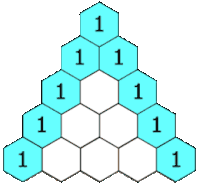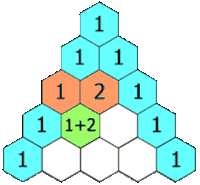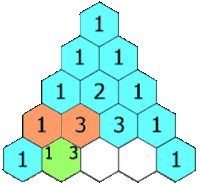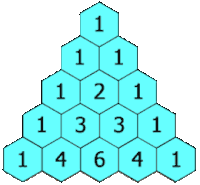
Fungovanie

Pascalova schéma funguje zhora. Začneme s jednou jednotkou a pod ňu napíšeme dve jednotky zľava a sprava. Ďalšie riadky zostrojíme tak, že na oba okraje napíšeme 1 a stredné čísla dostaneme ako súčet dvojice čísel v predošlom riadku priamo nad miestom, na ktorom práve sme. Napríklad 6 v piatom riadku dostaneme tak, že sčítame 3 + 3 zo štvrtého riadku.

Vlastnosti

Prvá a úplne zrejmá vlastnosť Pascalovho trojuholníka je jeho súmernosť. Trojuholník je osovo súmerný, teda ak jeho stredom vedieme zvislú čiaru, čísla napravo budú zrkadlovým obrazom čísel naľavo. Pod diagonálou zo samých jednotiek je diagonála z prirodzených čísel 1, 2, 3, 4, 5, 6, 7… (pozri obrázok vpravo hore). Pod ňou je zase diagonála z trojuholníkových čísel 1, 3, 6, 10, 15, 21… (čísla, ktoré sú počtom bodiek tvoriacich trojuholník). Pod touto diagonálou sú potom tetrahedrálne čísla 1, 4, 10, 20, 35…. Tieto potom zodpovedajú štvorstenom ("trojrozmerný trojuholník", alebo počty delových gulí poukladaných do tvaru pyramíd so zvyšujúcimi sa trojuholníkovými základňami).

Konštrukcia

{0 \choose 0}

{1 \choose 0}{1 \choose 1}

{2 \choose 0}{2 \choose 1}{2 \choose 2}

{3 \choose 0}{3 \choose 1}{3 \choose 2}{3 \choose 3}

{4 \choose 0}{4 \choose 1}{4 \choose 2}{4 \choose 3}{4 \choose 4}

{5 \choose 0}{5 \choose 1}{5 \choose 2}{5 \choose 3}{5 \choose 4}{5 \choose 5}

Vznik prvých šiestich riadkov podľa Pascalovho pravidla

Konštrukcia Pascalovho trojuholníka využíva Pascalovo pravidlo: ${n \choose k}={n-1 \choose k-1}+{n-1 \choose k}$

, kde n a k sú nezáporné celé čísla, pre ktoré platí že n≥k a kde ${n \choose 0}={n \choose n}=1.$ ^[1]^[2]

Referencie

↑ J. SMIDA, J. ŠEDIVÝ, J. LUKÁTŠOVÁ, J. VOCELKA. Matematika pre 1. ročník gymnázia. Bratislava: Slovenské pedagogické nakladateľstvo, 1990, [cit. 1990-11-11]. ISBN 80-08-00340-5.
↑ PETÁKOVÁ, J.. Matematika - příprava k maturitě a k přímacím zkouškám na vysoké školy. Praha: Prometheus, spol. s.r.o.,, 2000, [cit. 2000-11-11]. ISBN 80-7196-099-3. (český)

Zdroj

Crilly, T. Matematika 50 myšlienok, ktoré by ste mali poznať. Vydavateľstvo Slovart, 2011

Externé odkazy

Pascal's triangle (po anglicky)

Pozri aj

[1] J. SMIDA, J. ŠEDIVÝ, J. LUKÁTŠOVÁ, J. VOCELKA. Matematika pre 1. ročník gymnázia. Bratislava: Slovenské pedagogické nakladateľstvo, 1990, [cit. 1990-11-11]. ISBN 80-08-00340-5.

[2] PETÁKOVÁ, J.. Matematika - příprava k maturitě a k přímacím zkouškám na vysoké školy. Praha: Prometheus, spol. s.r.o.,, 2000, [cit. 2000-11-11]. ISBN 80-7196-099-3. (český)

[1]

[2]