Sínusová veta

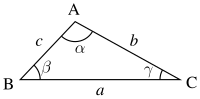
V trigonometrii je sínusová veta dôležité tvrdenie o rovinných trojuholníkoch. Najčastejšie znie takto:

Pre každý trojuholník ABC s vnútornými uhlami α, β, γ a stranami a, b, c platí:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R,$

kde R je polomer opísanej kružnice pre tento trojuholník. Čiže:
Pomer všetkých dĺžok strán a hodnôt sínusov im protiľahlých uhlov je v trojuholníku konštantný.
Alebo:
Pomer dĺžok strán trojuholníka sa rovná pomeru sínusov im protiľahlých uhlov:

${\frac {a}{b}}={\frac {\sin \alpha }{\sin \beta }},\quad {\frac {b}{c}}={\frac {\sin \beta }{\sin \gamma }},\quad {\frac {c}{a}}={\frac {\sin \gamma }{\sin \alpha }}$

Inak zapísané:

$a\sin \beta =b\sin \alpha ,\,$

$c\sin \beta =b\sin \gamma ,\,$

$c\sin \alpha =a\sin \gamma \,$

Použitie vety

• Máme dané dva uhly trojuholníka a dĺžku jednej jeho strany a chceme vypočítať veľkosť ostatných strán. To je typická úloha pri triangulácii.
• Poznáme dĺžky dvoch strán trojuholníka a veľkosť vnútorného uhla, ktorý nezvierajú a chceme vypočítať ostatné uhly. V tomto prípade sa však stáva, že nám veta poskytne dve riešenia (iba správne riešenie však poskytuje pri súčte všetkých uhlov v trojuholníku hodnotu 180°).

Pozri aj

• Kosínusová veta
• Tangensová veta
• Pytagorova veta
• Trigonometria

Externé odkazy

• Sínusová veta Archivované 2019-08-03 na Wayback Machine