Tálesova veta

Úsečka AC je priemer, uhol pri bode B má konštantnú veľkosť 90° (pravý uhol)

Tálesova veta: keď AC je priemer, potom uhol v bode B bude pravý.

V geometrii Tálesova veta (pomenovaná podľa gréckeho filozofa Tálesa z Milétu) hovorí, že ak A, B, C sú body na kružnici, kde AC je priemer kružnice, potom uhol ABC je pravý uhol.

Dôkaz

Obrázok ku dôkazu.

Pri dôkaze použijeme nasledovné tvrdenia:

• súčet vnútorných uhlov v trojuholníku sa rovná 180°,
• základňové uhly rovnoramenného trojuholníka sú rovnaké.

Nech $O$ je stred kružnice. Keďže platí $OA=OB=OC$, $OAB$ a $OBC$ sú rovnoramenné trojuholníky a na základe rovnosti základňových uhlov rovnoramenných trojuholníkov, $OBC=OCB$ a $BAO=ABO$. Označme uhly $\gamma =BAO$ a $\delta =OBC$. Tri vnútorné uhly trojuholníka $ABC$ sú potom $\gamma$, $\gamma +\delta$ a $\delta$. Súčet vnútorných uhlov každého trojuholníka je 180°:

$\gamma +(\gamma +\delta )+\delta =180^{\circ }$

z toho vyplýva po úprave

$2\gamma +2\delta =180^{\circ }\quad \Rightarrow \quad \gamma +\delta =90^{\circ }$,

čo bolo treba dokázať.

Zovšeobecnenie

Tálesova veta je špeciálnym prípadom nasledovnej vety:

Nech sú dané tri body $A$, $B$ a $C$ na kružnici so stredom $O$, potom uhol $AOC$ je dvakrát taký veľký ako uhol $ABC$.

Dôkaz tejto vety je podobný ako dôkaz Tálesovej vety uvedený vyššie.

Aplikácie

Konštrukcia dotyčnice kružnice

Konštrukcia dotyčnice využitím Tálesovej vety.

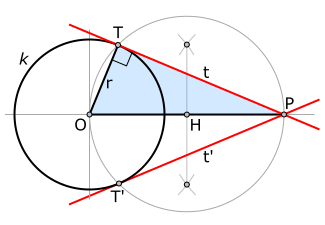
Tálesovu vetu môžeme použiť na konštrukciu dotyčnice danej kružnice, ktorá pretína daný bod (pozri obrázok). Nech je daná kružnica k so stredom O a vonkajší bod P mimo kružnice, chceme skonštruovať (na obrázku červenú) dotyčnicu (dotyčnice) kružnice k, ktorá pretína bod P. Označme bod, v ktorom sa (zatiaľ neznáma) dotyčnica t dotýka kružnice ako T. Zo symetrie je zrejmé, že polomer OT je kolmý na túto dotyčnicu. Nájdime stred H na úsečke spájajúcej body O a P a obkreslime kružnicu so stredom H cez tieto body. Podľa Tálesovej vety je hľadaný bod T priesečník tejto kružnice s danou kružnicou k, pretože to je bod na kružnici k, ktorý tvorí s bodmi O a P pravouhlý trojuholník OTP.

Pretože spomínané dve kružnice sa pretnú v dvoch bodoch, týmto spôsobom môžeme zostrojiť obe dotyčnice.

Určenie stredu kružnice

Ilustrácia: Určenie stredu kružnice použitím Tálesovej vety.

Použitím Tálesovej vety je možné nájsť stred kružnice pomocou objektu s pravým uhlom, napríklad listu papiera štvorcového alebo obdĺžnikového tvaru, ktorý je väčší ako kružnica. (Aspoň jedna strana objektu je dlhšia ako priemer kružnice, pozn. prekl.)

1. Vrchol pravého uhla umiestnime kdekoľvek na kružnicu (obrázok 1).
2. Pomocou priesečníkov strán pravého uhla s vrcholom na kružnici a kružnice vytvoríme úsečku – priemer kružnice (obrázok 2).
3. Postup zopakujeme s inou dvojicou priesečníkov a vytvoríme ďalší priemer (obrázok 3).

Stred kružnice sa nachádza v priesečníku vytvorených priemerov.

História

Táles nebol prvý, ktorý formuloval túto vetu, keďže Egypťania aj Babylončania ju poznali, pravdepodobne empiricky, pretože sa nenašli žiadne dokumenty s jej dôkazom. Veta je pomenovaná po Tálesovi, ktorému sa pripisuje jej prvý dôkaz. Táles použil svoje vlastné výsledky o základňových uhloch rovnoramenného trojuholníka a súčte vnútorných uhlov v trojuholníku.

Externé odkazy

• Kružnica a dotyčnica

Zdroj

Tento článok je čiastočný alebo úplný preklad článku Thales's_theorem na anglickej Wikipédii.