Matematické kyvadlo
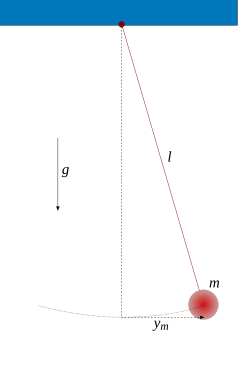
Matematické kyvadlo je matematickým modelom kyvadla. Matematické kyvadlo je hmotný bod zavesený na tenkom dokonale pevnom vlákne zanedbateľnej hmotnosti, pričom sa zanedbáva odpor vzduchu pri pohybe kyvadla i trenie v závese a gravitačné pole sa považuje za homogénne. Matematické kyvadlo je mechanický oscilátor, ktorý po dodaní počiatočnej energie voľne kmitá. Pri malých výchylkách (do ±5°) je priebeh tohto kmitania približne harmonický, možno ho vyjadriť pomocou funkcie sínus.
Matematický opis
[upraviť | upraviť zdroj]Na hmotný bod pôsobí len tiažová sila a ťahová sila vlákna, ktorá ho udržuje v stálej vzdialenosti od závesu. Veľkosť výslednej sily je
- ,
kde je tiažové zrýchlenie a φ je uhol, o ktorý je vlákno vychýlené z rovnovážnej polohy. Diferenciálna rovnica pre opis pohybu kyvadla je z 2. Newtonovho pohybového zákona
- ,
kde je dĺžka vlákna. Pokiaľ je maximálna výchylka z rovnovážnej polohy malá, možno funkciu sínus nahradiť lineárnou funkciou
- .
Diferenciálna rovnica má preto podstatne jednoduchší tvar
Táto rovnica má partikulárne riešenie
- ,
kde je počiatočná uhlová výchylka (predpokladáme nulovú počiatočnú rýchlosť, takže je to zároveň maximálna výchylka) a je čas, čo je pohybová rovnica harmonického oscilátora s periódou
- .
Periódu ovplyvňuje iba dĺžka kyvadla a tiažové zrýchlenie.
Pozri aj
[upraviť | upraviť zdroj]- Fyzikálne kyvadlo
- Torzné kyvadlo
- Kyv, kmit, Kmitanie
Zdroj
[upraviť | upraviť zdroj]Tento článok je čiastočný alebo úplný preklad článku Matematické kyvadlo na českej Wikipédii.











